Author: Rachel Lambert
-
How did Rethinking Disability and Mathematics shift secondary math teachers’ thinking?
Of course I have been wondering this since the book was published. Last week I heard from a group of secondary teachers in the Poway Unified School District who were reading it together on Friday afternoons (!) with Math TOSA Traci Jackson. She sent me their final reflections (with their permission):…
-
Game Time: An Intervention to Support Teachers and Students in Complex Times Learning Mathematics Through Joy
Presenters: Dr. Rachel Lambert (UCSB), Tomy Nguyen (Alder University, UCSB), Jenny Goldberg (UCSB) In an effort to bring joy to math intervention by using non-digital games that are fun and accessible for all students, whether or not they have been identified as being “in need of intervention,” we provided a…
-
The value of insider narratives
I love research. I do it, I write about it, and I read it daily. I absolutely love learning about education well studied. It is one way I learn about disability and neurodiversity. But I also have learned a tremendous amount from people in my circle: family, neighbors, friends, and…
-
Resources for Webinar
Here are the resources I mention for today’s webinar on Unpacking Research Claims About the Teaching and Learning of Mathematics with NCTM. https://www.nctm.org/online-learning/Webinars/Details/686 Description: Multiple documents exist to help math teachers understand the research behind teaching and learning mathematics, from the CCSS to IES practice guides. Increasingly, math educators face…
-
UDL Math!
I am super excited to share a article I wrote proposing UDL Math. It is published in the September issue of Teaching and Learning Mathematics K-12. You can access it here for NCTM members and below for those who are not yet NCTM members. I have long wanted to develop…
-
13 thoughts on math teaching and intervention as we enter the 2021 school year
I have trying to write this post all summer. Each time I try, I want it to be more focused. Yet each time I revisit this idea I feel there are more things to add! So here we are, with the cumbersome number of 13 thoughts on math teaching as…
-
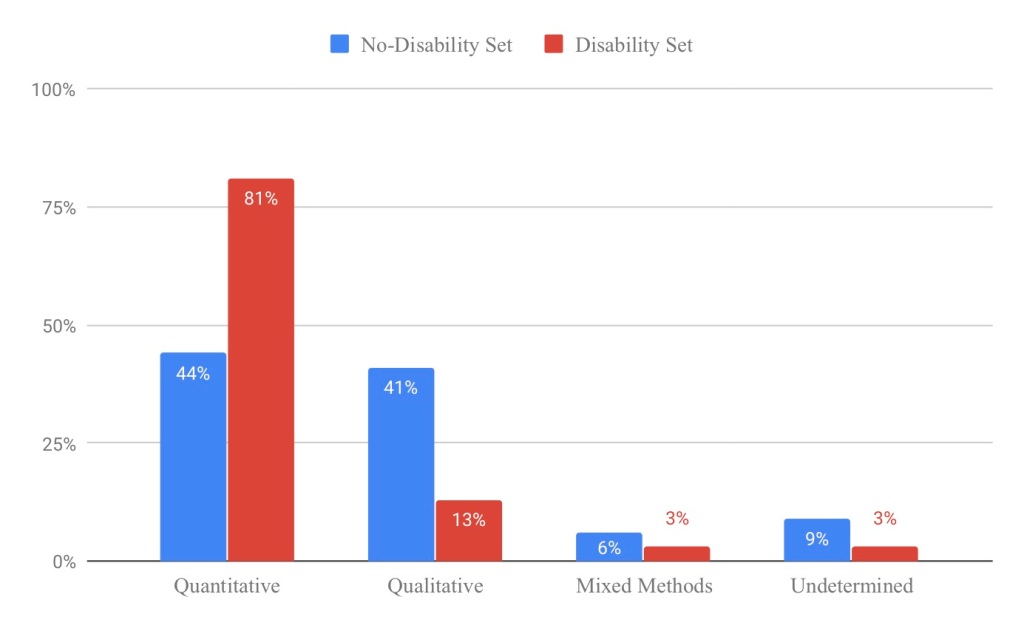
Research Breakdown: What is different in math research for students with and without disabilities; an article that took 8 years to get published!
To call this a new article is a bit of a stretch. I first started writing this article in 2013. I planned to write a Research Commentary for JRME (a fancy math ed journal) on what I saw as the stark differences between 1) math ed research and 2) special…
-
Research Breakdown: Teaching Math to SwD during Emergency Remote Teaching
Just uploaded a preprint (before peer review, so not final!) of a study I did this spring with Rachel Schuck, a doc student at UCSB in Special Education. I was working on a research study on UDL with some exceptional special educators. After schools were closed, some of the teachers…
-
Research Breakdown: My article on how disability in mathematics is political, relational, emotional and complexly embodied (Lambert, 2019)
Part of my intention with this blog is to provide access for a wide audience on research into disability in the context of mathematics. Research is too inaccessible; hard to get the articles and hard to understand them even when you do get your hands on them! Today I want…
-
Intervention in Participation
On Saturday, 11/5/16 I did a presentation at PME-NA in Tucson about a research review I recently did on increasing the participation of students with LD in mathematical problem solving and discussion. The basic idea is this: why is intervention in mathematics always focused on content. Could we also design intervention in…
mathematizing4all 